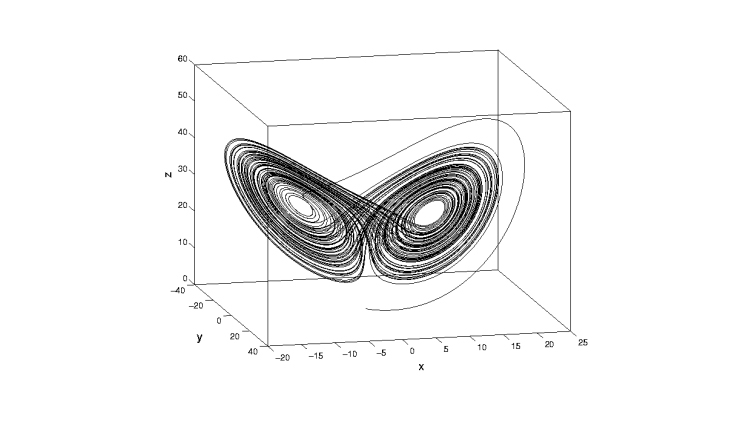
« Les attracteurs étranges ont été mis en évidence pour la première fois par Edward Lorenz en 1963. Ils tiennent leur curieuse dénomination du fait qu’ils ne sont ni des courbes ni des surfaces. Ils sont la représentation des états de systèmes dits « chaotiques », c’est-à-dire indéterminables car trop dépendants des conditions initiales. Ces systèmes (un nuage, la macroéconomie, une entité biologique) agissent a priori de manière désordonnée mais ils obéissent malgré tout à des contraintes déterministes qui sont inaccessibles à notre entendement car infiniment nombreuses et complexes. Ces contraintes déterministes existent pourtant et se révèlent dans la figure des attracteurs qui forme en quelque sorte le « lit » ou le « moule » dans lequel semble attirée la dynamique d’un système chaotique. »
(Otto – L’Homme réécrit, Marc-Antoine Mathieu, note de fin d’ouvrage)
Dans la théorie du chaos, le chaos n’est pas le désordre mais l’ordre fluctuant qui s’établit entre des éléments en interaction. Les systèmes complexes (écosystème, organisme, société, cerveau, univers…) sont des systèmes chaotiques dont l’équilibre est dynamique et non statique.
Lorsque l’état du système est tangent entre plusieurs évolutions possibles, des événements infinitésimaux peuvent entraîner des conséquences en chaine qui peuvent s’avérer déterminantes.
Dans l’étude des systèmes dynamiques, un attracteur (ou ensemble-limite) est un ensemble ou un espace vers lequel un système évolue de façon irréversible en l’absence de perturbations. Par exemple, le fleuve est un attracteur du bassin fluvial.
« Un système caractérisé par un cycle limite reste un système prévisible, que l’on peut décrire de manière simple. […] Jusqu’à ces dernières années, on croyait que les seuls attracteurs possibles correspondaient à des variétés continues, telles que lignes, surfaces et volumes. Mais la découverte des « attracteurs étranges » a ouvert des nouvelles. Les attracteurs étranges ne sont pas caractérisés par des dimensions entières, comme une ligne ou une surface, mais par des dimensions fractionnaires. Ce sont ce que, depuis Mandelbrot, on appelle des variétés fractales. […] Jusqu’à il y a peu, l’existence d’un attracteur avait été synonyme de stabilité et de reproductibilité : retour au « même » malgré les perturbations, quelles que soient les particularités initiales. Aux nouveaux types d’attracteurs correspondent des comportements « sensibles aux conditions initiales » qui font perdre son sens à la notion de « même ». Dans toute région, aussi petite soit-elle, occupée par l’attracteur fractal, passent autant de trajectoires que l’on veut, et chacune de ces trajectoires connaît un destin différent des autres. En conséquence, des situations initiales aussi voisines que l’on veut peuvent engendrer des évolutions divergentes. La moindre différence, la moindre perturbation, loin d’être rendue insignifiante par l’existence de l’attracteur, a donc des conséquences considérables. (…) Nous arrivons ici à la définition du comportement « chaotique », qui est un comportement typique des systèmes caractérisés par un attracteur étrange. Un comportement est chaotique si des trajectoires issues de points, aussi voisins que l’on veut dans l’espace des phases, s’éloignent les unes des autres au cours du temps de manière exponentielle ; la distance entre deux points quelconques appartenant à de telles trajectoires croit proportionnellement à une fonction exponentielle de l’inverse du temps de Lyapounov. Le temps de Lyapounov permet de définir une véritable « échelle de temps ». »
(Entre le temps et l’éternité, Ilya Prigogine et Isabelle Stengers)
« Dans les systèmes plus complexes dont l’évolution est « imprédictible », comme par exemple le chemin suivi par deux feuilles mortes tombant d(un même point de départ, les trajectoires vont se séparer pour devenir totalement dissemblables. Cette caractéristique d(amplification des écarts entre trajectoires de l(espace des phases a été nommée sensibilité aux conditions initiales. Lorsque cette propriété existe, le système correspondant est considéré comme chaotique.
Le tracé représentant l’évolution d’un système chaotique dans l’espace des phases en fonction du temps se comporte de manière « étrange » par rapport aux attracteurs des systèmes simples comme nous l’avons vu plus haut, c’est pourquoi D. Ruelle l’a nommé « attracteur étrange », ajoutant qu’il considérait sa propre expression comme « psychanalytiquement suggestive » (G. Pragier et S. Faure-Pragier, 1990, p. 1443).
Comme l’expliquent M. Dubois, P. Atten et P. Bergé (1987), le caractère étrange d’un tel attracteur vient du fait que « sa structure doit refléter deux tendances apparemment antagonistes : l’attraction des trajectoires vers l’attracteur et leur divergence sur ce dernier. L’attraction est liée au caractère dissipatif de tout système réel : sous l’effet des forces de frottement, les trajectoires tendent à venir se rejoindre sur l’attracteur. La divergence vient, quant à elle, de la sensibilité aux conditions initiales. La cohabitation de l’attraction et de la divergence apporte une contrainte d’autant plus forte que les trajectoires doivent être décrites continûment (puisqu’elles représentent une dynamique à tout moment), dans un espace confiné (puisque les valeurs des variables, vitesse, angles, etc. du système sont nécessairement limitées) et enfin qu’elles ne peuvent se couper (déterminisme) » (p. 196).
La divergence exponentielle des deux trajectoires reste cependant un phénomène local, et comme les attracteurs ont des dimensions finies, il est impossible que les deux trajectoires divergent de manière infinie, de sorte que l’attracteur doit se replier sur lui-même à un moment ou à un autre. En d’autres termes l’attracteur étrange est le résultat de trois opérations simultanées – contraction, étirement et repliement – qui vont donner naissance à une structure caractéristique en forme de fer à cheval qui va être à son tour aplatie, étirée et repliée. L’attracteur est ainsi fabriqué d’une manière analogue à celle utilisée par le boulanger pour mélanger sa pâte, de sorte qu’il présente une structure feuilletée, « la trajectoire s’emboîtant à l’intérieur d’elle-même à des échelles de plus en plus petites, puisqu’elle ne repasse jamais au même endroit. On retrouve là le concept d’autosimilarité d’un objet fractal » (ibid. p. 198).
Ainsi, les trajectoires d’un attracteur étrange possèdent également les caractéristiques d’un objet fractal, c’est-à-dire d’un objet qui présente une structuration qui reste du même type quelle que soit l’échelle à laquelle on la regarde. Ce caractère fractal est donc une propriété générale des attracteurs étranges. Il résulte de ce qui précède que, dans un espace ayant au moins trois dimensions (ou davantage), un système dynamique non-linéaire peut devenir chaotique. Comme le résument M. Dubois, et coll. « la propriété de sensibilité initiale est donc génératrice de chaos, chaos dont la signature est la présence d’un attracteur étrange dans l’espace des phases. C’est cette signature qui permet d’authentifier un comportement chaotique et de la caractériser quantitativement » (ibid. p. 197). »
(Quinodoz)